How to calculate cross product and dot product of two vectors?

Vector multiplication is a headache for students of Physics and Mathematics because it is a bit tricky to find product of vectors. You can benefit from online cross product calculator , factorial calculator as well as dot product calculator, if you are not a math geek.

Read more: Content Writing Secrets: Become a Content Writing Expert

However, in this post, we will explain how to calculate cross product of two vectors as well as dot product.

When talking about vector product, only two type of products come into mind.

1. Dot product
2. Cross Product

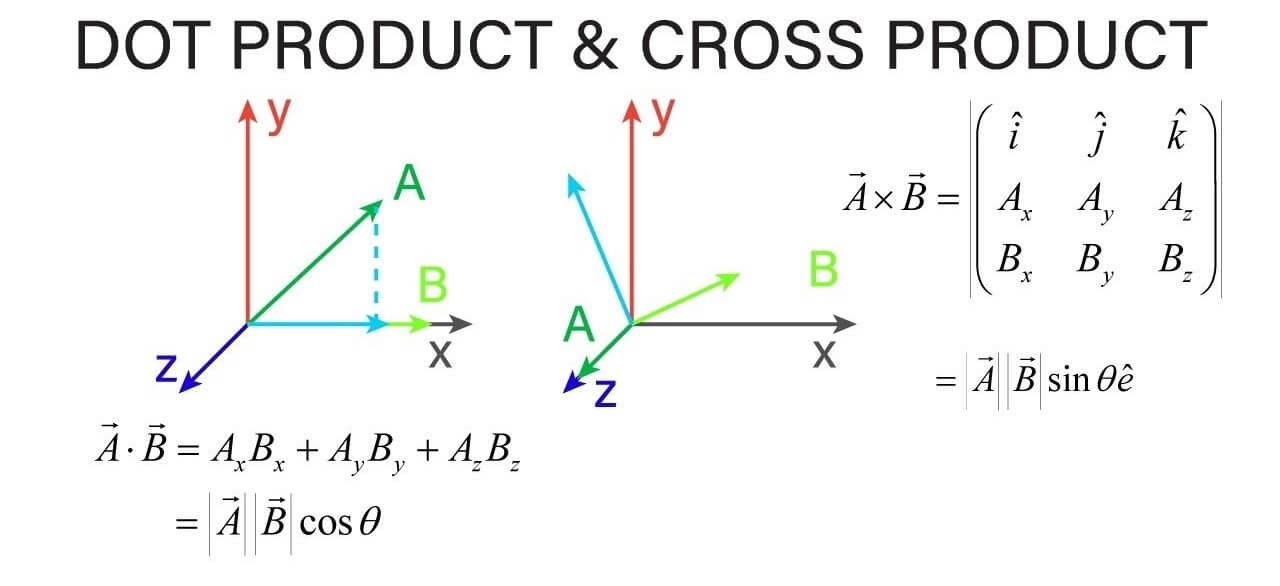
What is Dot Product?

The dot product also referred to as scalar product is an algebraic operation that takes two equal-length sequences of numbers, and returns a single number.

What is Cross Product?

Wikipedia defines cross product as,

The cross product is a binary operation on two vectors in three-dimensional space and is denoted by the symbol “x“. Given two linearly independent vectors a and b, the cross product a × b is a vector that is perpendicular to both a and b.

The direction of cross product can be found by applying the right hand rule.

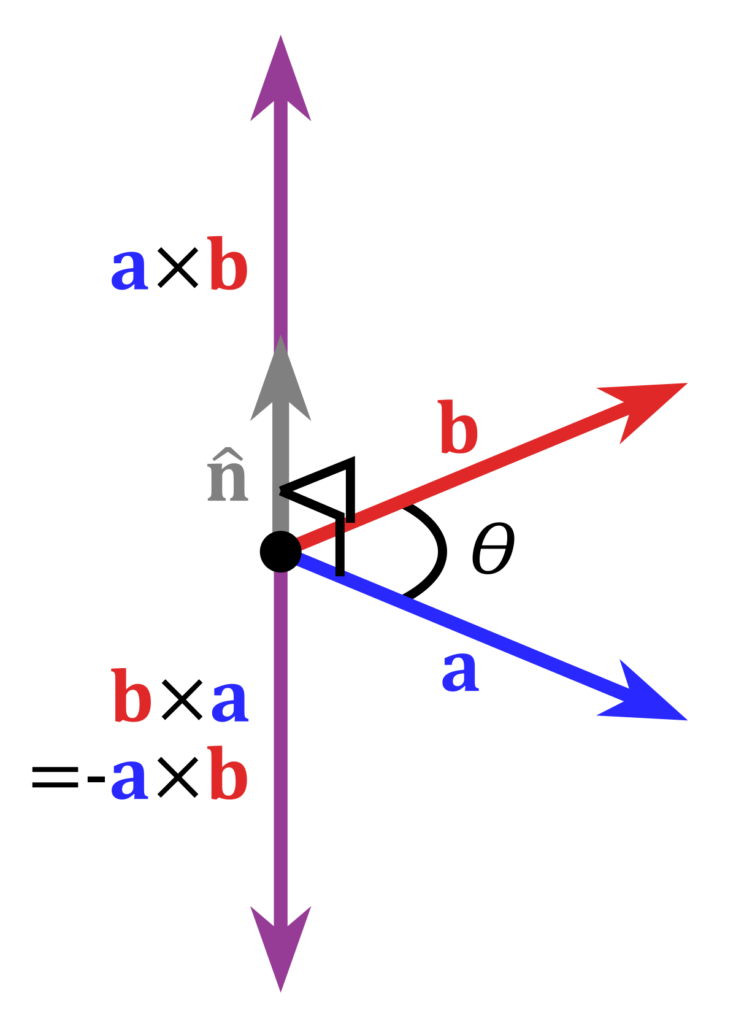
How to calculate cross product of two vectors?

To find the cross product, use the below formula.

(a_i a_j a_k) × (b_i b_j b_k) = (a_j × b_k – a_k × b_j    a_k × b_i – a_i × b_k    a_i  b_j – a_j × b_i)

Example:

Find the cross product of two vectors a(2i, 1j, 4k), and b(3i, 2j, 1k).

Place the values in formula of cross product.

(a_i a_j a_k) × (b_i b_j b_k) = (1 × 1 – 4 × 2    4 × 3 – 2 × 2    2 × 2 – 1 × 3)

a × b = (1-8    12-4      4-3)

a × b = (-7     8     1)

a × b = 7i   8j   1k

How to calculate cross product of two vectors?

To find the dot product of two vectors, use the below dot product formula.

(a_i a_j a_k) ∙ (b_i b_j b_k) = (a_i ∙ b_i + a_j ∙ b_j + a_k ∙ b_k)

Example:

Find the dot product of two vectors a(2i, 1j, 4k), and b(3i, 2j, 1k) given in above example.

Place the values in formula of dot product.

(a_i a_j a_k) . (b_i b_j b_k) = (2∙3 + 1∙2 + 4∙1)

a ∙ b = (6 + 2 + 4)

a ∙ b = 12